2. RISK VBox¶
Software for automated Credit Risk Management and Reporting.
Accurate and standard compliant with IFRS 9 and Basel II+III.
High performance for large portfolios of more than 10 Million accounts.
2.1. Data Management¶
Since Banks do not always have all data electronically available, the Software provides its own Business Object Schema to capture and manage Credit Risk related data such as:
Counter parties (in different roles, e. g. Obligor, Guarantor, Collateral Provider, Beneficiary)
Financial Assets
Collaterals
Issuer and Issue Rating (Intern or Extern)
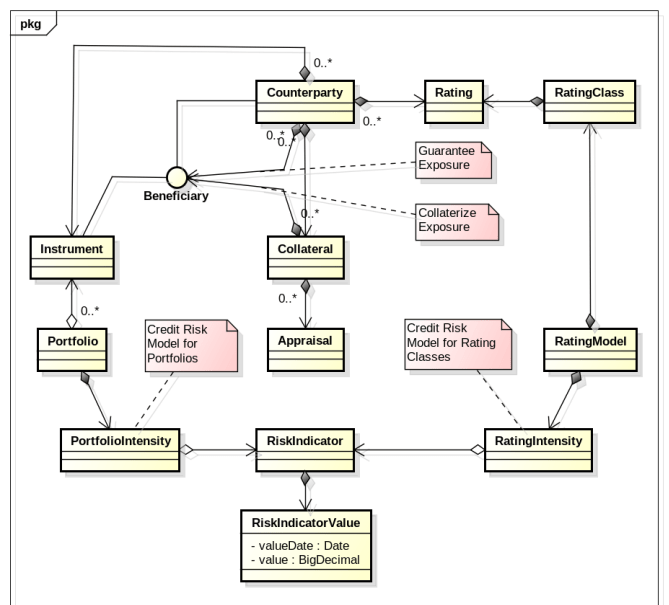
Credit Risk Business Object Model¶
2.2. Credit Risk Modelling¶
Forward Looking Information¶
Management of Macro-Economic Covariates and Forecast of Time Series. RISK VBox supports the following Forecast methods:
ARIMA
Holt-Winters
Prophet
Feed-forward Neural Network
Probability of Default (PD)¶
Analysis of Observed Losses Through the Cycle using a Markov-Model.
The Markov Model is a mathematical model used to represent the evolution of a system over time. It is based on the idea of a Markov process, which is a type of random process that satisfies the “memoryless” property, meaning that the probability of transitioning to a future state is dependent only on the current state and time elapsed, and is not influenced by the past states.
In a Markov model, the system is assumed to be in one of a finite number of states at any given time. The transitions between states are governed by a set of probabilities, which specify the likelihood of transitioning from one state to another. These probabilities are typically represented in a transition matrix, which is a matrix of size N x N, where N is the number of states.
Markov models are often used to model systems that change over time and involve a certain level of randomness or uncertainty. They are widely used in a variety of fields, including economics, biology, and computer science, to analyze and predict the evolution of systems over time.
Overall, a Markov model is a useful tool for representing and analyzing the evolution of systems that change over time and involve a certain level of randomness or uncertainty. It is particularly useful for modeling systems in which the future state is only dependent on the current state and time elapsed, and is not influenced by the past states.
Transformation into Point in Time Curves using a Proportional Hazards Model (“Cox Model”).
The Proportional Hazards Model is a statistical model used to analyze the relationship between a dependent variable (such as time to an event) and one or more independent variables. It is a type of survival analysis model, which is used to analyze data in which the time until an event of interest (such as death or failure) is of primary interest.
The Cox model is based on the idea that the hazard rate, which is the probability of the event occurring at a given time, is proportional to the risk of the event. The hazard rate is modeled as a function of the independent variables, with the coefficients of the independent variables representing the effect of each variable on the hazard rate.
The Cox model can be used to estimate the relative risk of an event occurring, as well as to predict the likelihood of an event occurring based on the values of the independent variables. It is often used in medical research to analyze data on survival times, but it can also be applied to other types of data in which time to an event is of interest.
As per Rating Class (for Corporate Lending, when Obligor Rating is available)
As per Portfolio (for Retail Lending based on Behavioral Patterns and Scores)
Recovery¶
Analysis of the Cash Recovery after Default, considering actual Sale of Collaterals and Write-offs or Modification Losses. Calculates Cure Rate, Recovery Rate and Redefault Rate over time as per Portfolio — adjusted by Forward Looking Information.
Credit Conversation Factor¶
Roll-Rate Analysis of Undrawn Portions before Credit Events.